Normalizing biomechanical data

📝 Weekly paper summary

Comparison of 5 Normalization Methods for Knee Joint Moments in the Single-Leg Squat (Hirsch et al., 2022)

Comparison of 5 Normalization Methods for Knee Joint Moments in the Single-Leg Squat

Ratio scaling is the most common magnitude normalization approach for net joint moment (NJM) data. Generally, researchers compute a ratio between NJM and (some combination of) physical body characteristics (eg, mass, height, limb length, etc). However, 3 assumptions must be verified when normalizing…

Human KineticsSteven M. Hirsch

(yes, one of my papers this week, which is related to one of my previous blog posts on the topic of normalizing biomechanical data 😊)

Context

It's common in many analyses to divide an outcome variable (such as a net joint moment [NJM]) by an explanatory variable (people's body mass) to "level the playing field." However, anytime a ratio like this is computed, there are several latent statistical assumptions that researchers (and practitioners) must also consider. I highlighted these assumptions in more detail in my previous blog post, but the three we explored in this paper are as follows:

1) The Intercept Assumption

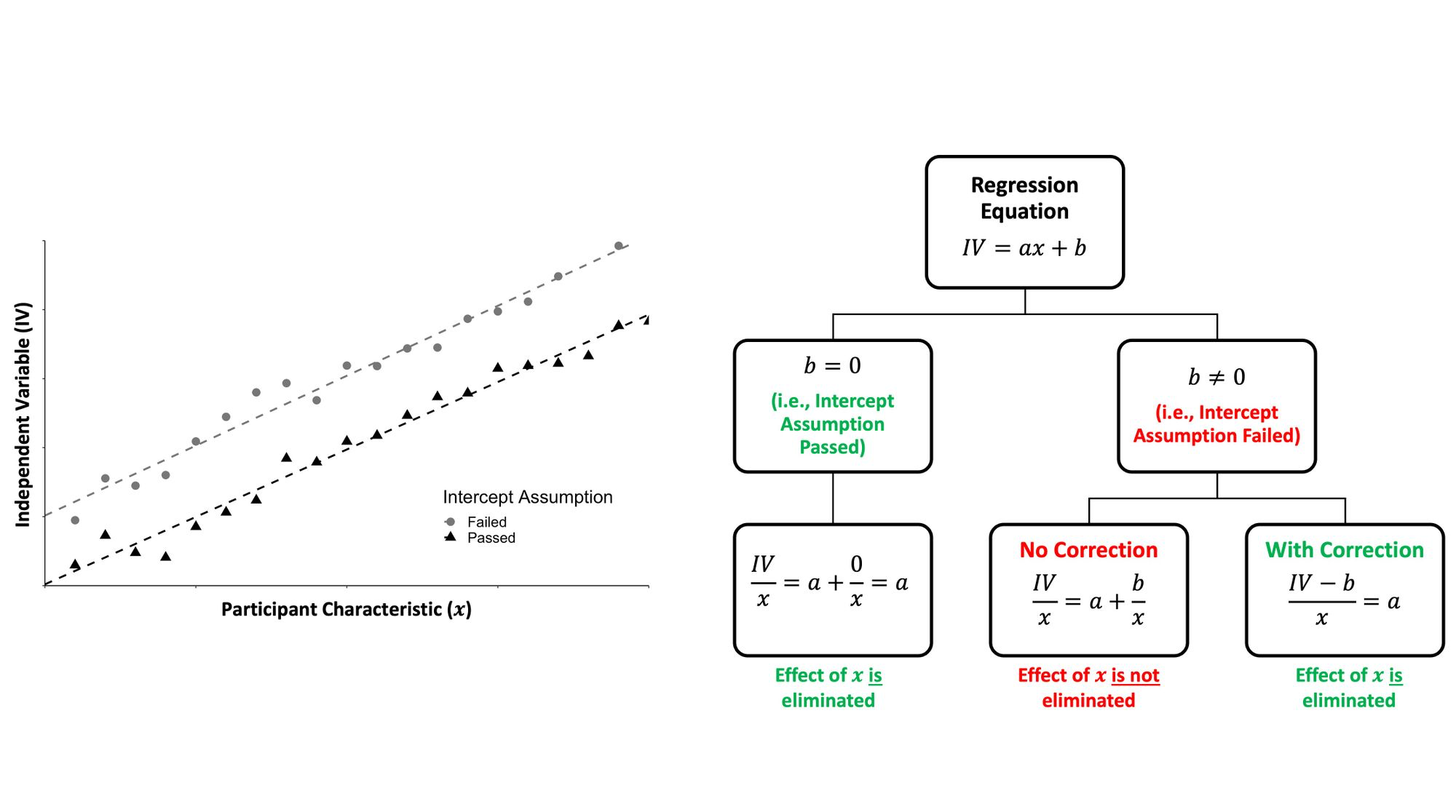
A visual depiction of the intercept assumption. If the intercept of the regression line between a participant characteristic (e.g., body mass) and an independent variable (e.g., an NJM) does not pass through the origin, then a correction factor would need to be applied to the independent variable before computing the ratio to eliminate the effect of the participant characteristic.

2) The Correlation Assumption

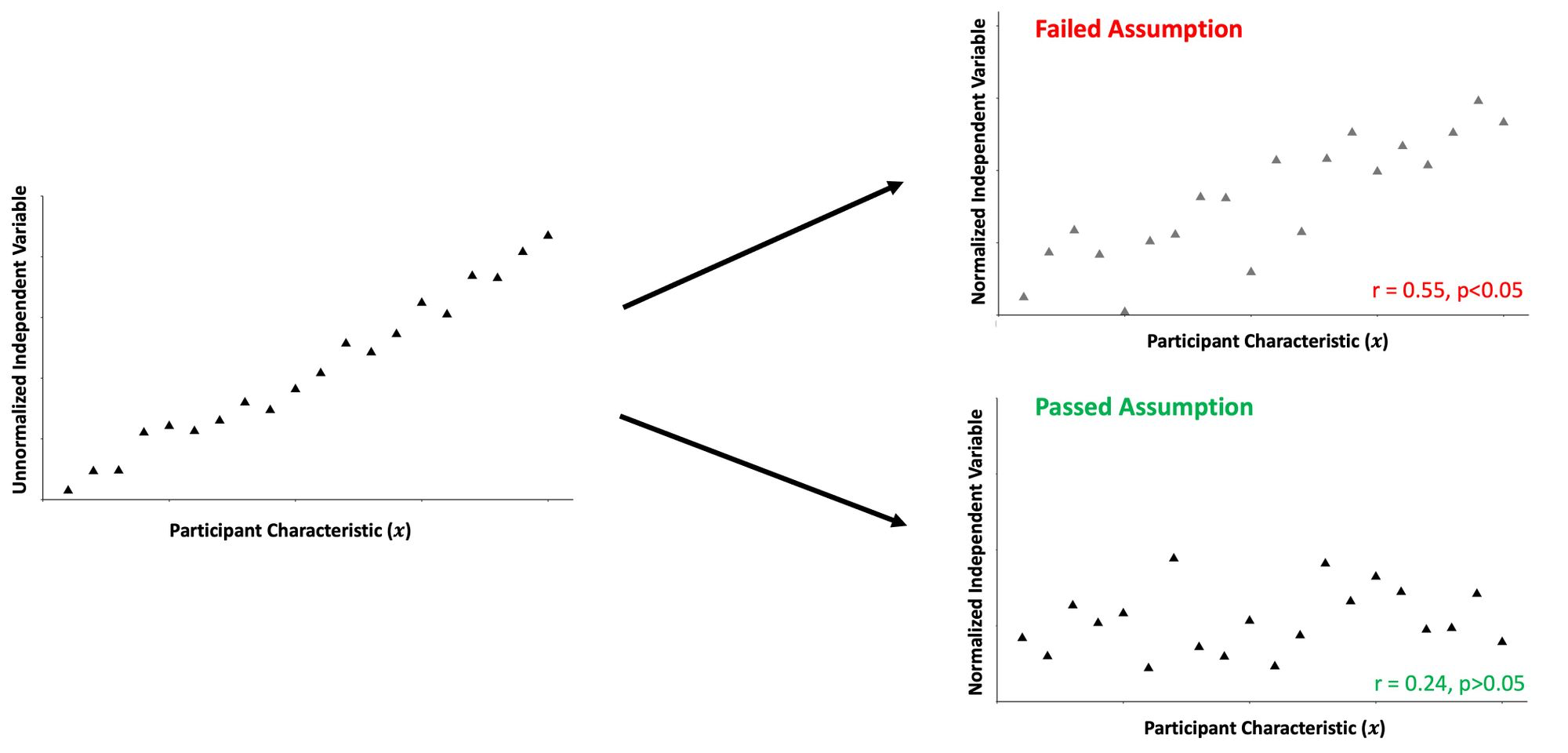
A visual depiction of the correlation assumption. If a significant proportion of the variance in the normalized variable (e.g., NJM/mass) is still explained by a participant characteristic (e.g., mass), then we aren't accomplishing our objectives of accounting for the variability between people of different body shapes and sizes.

3) Statistical Difference Assumption

The statistical difference assumption implies that the interpretations of whether statistically significant differences exist between groups are the same when computing ratios as when one computes a linear model adjusting for participants' body shapes and sizes. For example, suppose the inferences from a linear model comparing the NJM between two groups that adjusts for participants' body mass gives a different answer than comparing the NJM/kg between these two groups using a t-test. Assuming that the linear regression assumptions were satisfied, we have an inconsistency that needs resolving (and we're better off going with the linear regression).

The study's purpose was to assess these three assumptions when normalizing knee NJM data during a single leg squat. We hypothesized that normalizing this data using the product of mass*height or mass*leg length would satisfy all three assumptions since the units would be more dimensionally similar to NJM data.

Correctness

I'm pretty biased with this study and think we did lots of things well, so let me highlight some of the more relevant delimitations that you should consider when interpreting these data (you can find a complete list in the paper):

these findings are somewhat specific to the modelling decisions made in this investigation since different filter cutoff frequencies, the use of functional joint centers, etc. could impact joint kinetics
We tested people in a narrow band of movement velocities during a single-leg squat. Therefore, the appropriateness of the normalization techniques could conceivably change depending on the movement velocities and magnitude of joint excursions when performing a task (e.g., the results may be different when interpreting running data)
Other joints, with more or less ranges of motion and joint dynamics, may also yield different results.

Contributions

Normalizing NJM about the mediolateral axis (i.e., flexion/extension moments): mass*height and mass*leg length satisfied all three assumptions, but mass, height, and leg length alone did not
Normalizing NJM about the anteroposterior axis (i.e., ab/adduction moments): height and leg length satisfied all three assumptions, but mass, mass*height, and mass*leg length did not

🧠 Fun fact of the week

Blue whale calves grow about 200lbs per day every single day for the first year of their life! That's 73,000lbs (~33,000kg) in a year!

Photo by guille pozzi / Unsplash

🎙 Podcast recommendation

🗣 Quote of the week

I am patient with stupidity but not with those who are proud of it.

- Edith Sitwell

This one is especially relevant to the times right now :). IYKYK.